The Groundwater Mounding Calculator is solving the Hantush analytical equation (Hantush, 1967) for groundwater mounding beneath an infiltration basin.
The Hantush equation incorporates simplifying assumptions, including that the aquifer is homogeneous and isotropic, all flow is horizontal, the infiltration rate is constant and the change in saturated aquifer thickness is trivial relative to the original saturated thickness. Therefore, vertical anisotropy is not accounted for with the Hantush equation and the height of groundwater mounding is underestimated, where vertical anisotropy is present (Carleton, 2010). To account for vertical hydraulic anisotropy and vertical flow, a finite-difference numerical flow model such as MODFLOW is recommended (see T03. MODFLOW-based Model Setup). If storage in the unsaturated zone or delayed yield from the unsaturated zone occurs, the Hantush equation overestimates the resulting groundwater mound (Carleton, 2010).
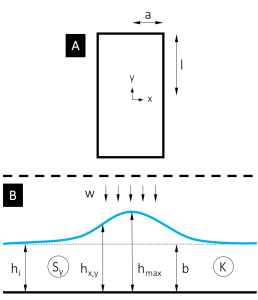
The online calculator accepts user-supplied values for horizontal soil permeability (K), initial saturated aquifer thickness (hi), specific yield Sy, half-length of the recharge basin (l), half-width of the recharge basin (a), and duration (t) and magnitude (w) of recharge rate.
The equation to calculate the groundwater mound is as follows:
| (eq. 1) |
where
| (eq. 2) |
and
| hx.y,t | = height of water table above impermeable layer at x, y, and time t [L]; |
| hi | = initial height of water table above impermeable layer [L]; |
| w | = arrival rate at water table of water from infiltration basin or basins [L/T]; |
| t | = time since start of recharge [T]; |
| Sy | = specific yield [-]; |
| = diffusivity [L²/T], where |
|
| l | = half-length of recharge basin or recharge project area (in y direction) [L]; |
| a | = half-length of recharge basin or recharge project area (in x direction) [L]; |
| b | = average aquifer thickness [L]; |
| y | = distance from the center of the recharge basin in the y direction [L]; |
| x | = distance from the center of the recharge basin in the x direction [L]; |
| = dummy variable of integration; and | |
| = error function. |
Example
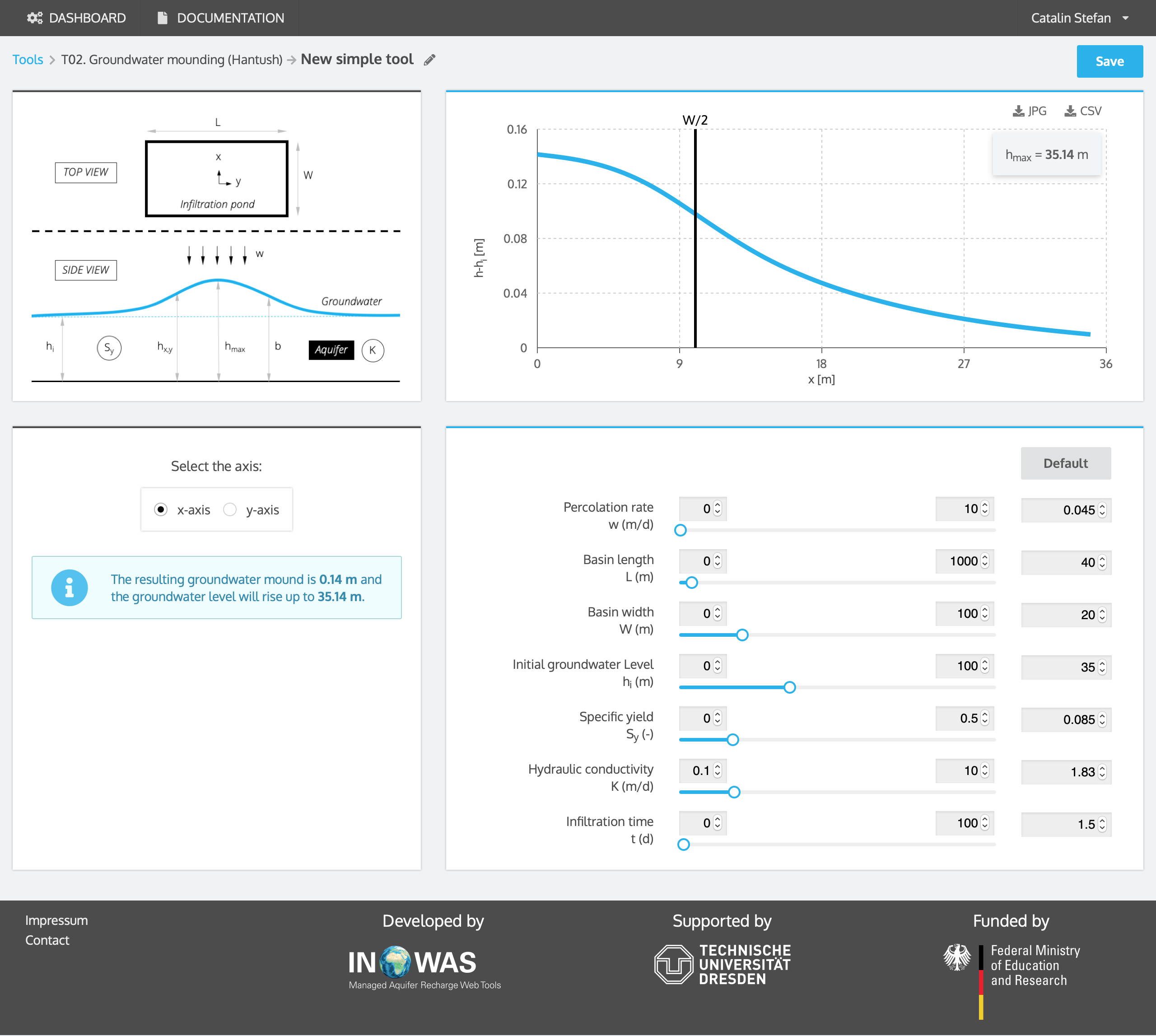
An infiltration basin of size 40 m x 20 m is planned to be build to inject water when it is available to increase groundwater storage. The aquifer has a specific yield Sy of 0.085, a hydraulic conductivity K of 1.83 m/d and the initial aquifer thickness hi is 35 m. The groundwater depth before the start of the infiltration is 15 m below land surface. In the course of infiltration, the groundwater is not allowed to rise above 12 m below land surface. The recharge rate w is projected to be 0.045 m/d over a duration of 1.5 days. With the help of the Hantush equation, the aquifer mounding can be calculated which equals 0.14 m. Therefore, the groundwater table will rise up to 14.86 m below land surface in the centre of the recharge basin, which is smaller than the maximum allowed rise.
References
- Hantush, M.S. (1967). Growth and decay of groundwater-mounds in response to uniform percolation. Water Resources Research, 3(1):227-234.
- Carleton, M.D., 2010. Simulation of Groundwater Mounding Beneth Hypothetical Stormwater Infiltration Basins, U.S. Geological Survey Scientific Investigations Report 2010–5102, 64 p.
